見たことないかも「放物線定規」便利な!?三角関数テンプレート付き
こんにちは、クリポンです。
普段どんな定規を使っていますか。定規といえば基本は直線定規。あとは昔学校で使った三角定規もありますね。
私が日常的に使うのは直線定規くらいでしょうか。自称文房好きと言っているものの、定規のコレクションはしていなくて。そもそも定規について深く考えたことがなかったなあ…。しかし先日、ちょっと珍しいものを見つけて、購入してみました。
今回は日本ではなかなか見ることのない!?海外の「放物線定規」についてお届けします。
こんなものがあったとは! 実際に使ってみた「放物線定規」
数学の理解が深まるかもしれない!?変わった定規
どうやって使うのだろう…と一瞬、頭をひねってしまう定規です。

放物線、さらには三角関数の曲線が描ける定規です。定規と言うより、テンプレート(同じ形が何回でも描ける型のこと)と言った方が良いかもしれません。実際、ヨーロッパではテンプレートの名で売られています。
学生用の定規
一口に定規と言っても、その形種類は多様です。アートや設計、建築その他いろいろ、専門家が使う特別仕様のものもあります。
今回取り上げる上の写真のものは、どこか可愛らしさがあると思いませんか。そう、子供が学校で使う定規なんです。
とはいえ放物線、三角関数用なので、子供というより中高生と言った方が良さそうです。
主にドイツで使われているらしい
日本では手に入れにくい放物線定規ですが、実はたくさんのメーカーが製造しています。私の住むフランスでは、ネットなどで簡単に手に入れられます。
でもこの定規、売られている割には、フランスの学校ではあまり使われていないように思います。

一体、この定規はどこで使われているのだろう?と気になり、ちょっと調べてみました。どうやら、ドイツでよく使われているようです。学用文具として指定される定規なのかもしれません。
さらに分かったのは、この「放物線定規」兼「三角関数テンプレート」を販売しているのは、ほとんどがドイツメーカーであることです。私が見つけた販売メーカーをざっと挙げてみます。
放物線定規の販売メーカー
ドイツ
- WEDO
- Faber-Castell
- Herlitz
- STYLEX
- BRUNNEN
- Idena
- KUM
- M+R/Moebius-Ruppert
- ARISTO
- TSI
デンマーク
- LINEX
ベルギー
- Q-Connect
上のリストの中で、日本では「WEDO」のものが購入できるようです。
こんな↓数学系定規についても書いています。

使ってみよう!「放物線定規」
この定規で何ができるの?と気になりますよね。私がみた感じでは、以下の3つのことが可能なようです。
|
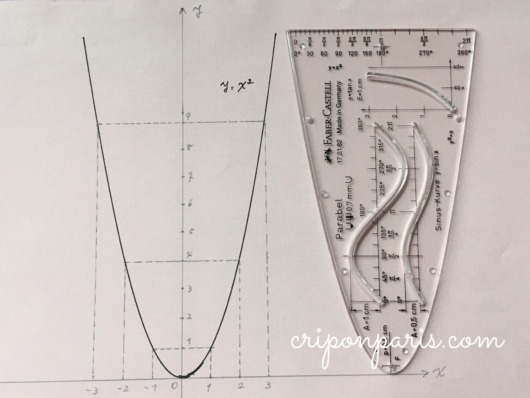
1. y = x2 の放物線
定規の形をなぞってみました。するとどうでしょう、y = x2の放物線になりました。
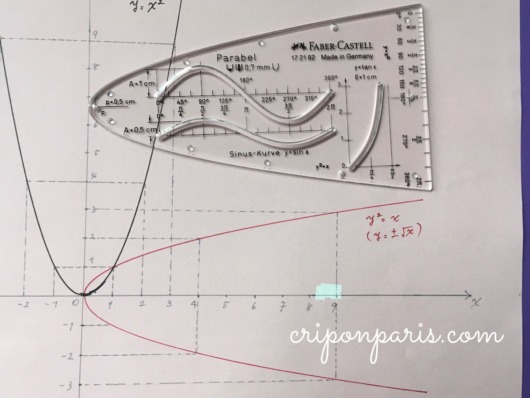
下の写真のように、定規を横に倒して描けば、y2=xのグラフ(赤線)になります。
(山の形のてっぺんを上向きにすればy=-x2に、右向きにすればy2=-xになります)
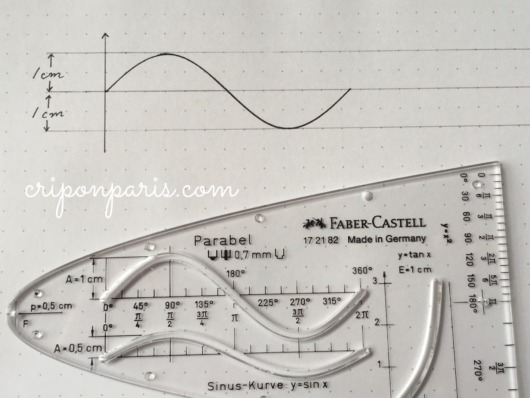
2. sinの曲線(正弦曲線)
海外の放物線定規は、しばしば三角関数のテンプレートとしても使えます。
下の写真は、三角関数のうち「sin サイン」の曲線(サインカーブ)です。

2種類の振幅(1cmと0.5cm)を描くことがが可能です。このうち、上の曲線(振幅1cm)を使ってみました。
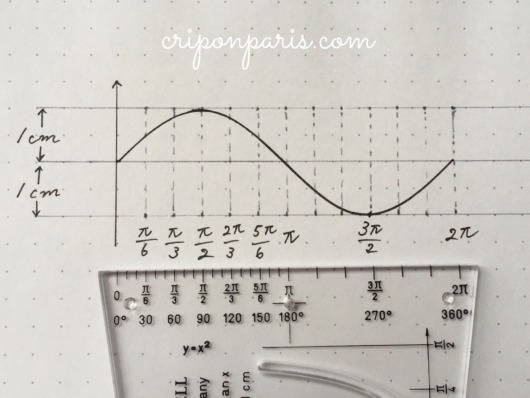
ここまで描いたら、定規の底辺部の出番です。

ラジアン(円の角度を表す値)の目盛りが付いています。実はこの目盛りはテンプレートの曲線に対応しており、グラフを書くときに役立ちます。
底辺部で測りながら、細かく線を引いてみました。
さらに曲線の横にコンパスで円(単位円)を描けば、円との対応関係が視覚的に明らかになります。

コサインの曲線ももちろん作成できます。少し手間がかかりますが、上のサインカーブを2つ繋げて描いて、-π/2平行移動させればコサインカーブになります。
3. tangentの曲線(正接曲線)
こちらは「tangent タンジェント」の曲線。上半分(yの値が正になる部分)のみです。

まずはこのまま描いてみました。
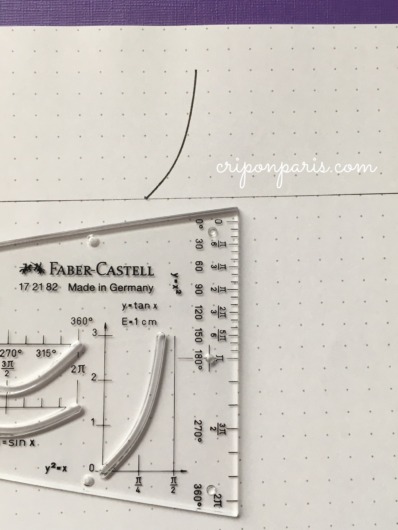
定規を逆さまにして線の続きを加えます。立派なタンジェントの曲線になりました。

ここでも、定規の底辺にある目盛りを使います。測りながら縦線を入れていき、タンジェントの曲線を増やして完成させたのがこちらです。
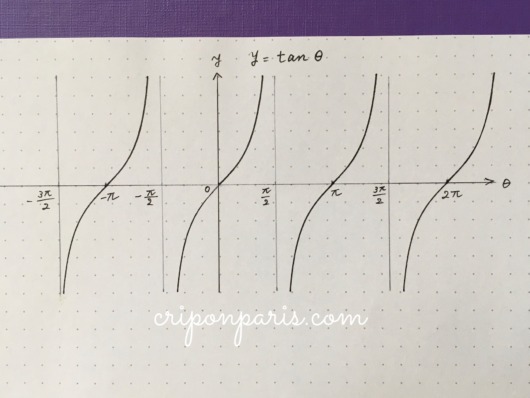
手書きで綺麗に描くのが難しいタンジェントですが、定規を使えば簡単です(と言いながら微妙にずれてしまいましたが…)。
子供の頃にあればよかった定規
海外で使われている放物線定規をご紹介しましたが、数学を勉強するうえで持っていた方がいい物なのかと言われると、個人的には特に必要性を感じません。例えば学校の宿題でグラフをかくことがあれば、便利かもしれません。でもこういうグラフって何回も書く機会があるわけではないし、グラフは綺麗に書こうが手書きで多少乱れていようが、要は内容を理解することですからね。まあでも面白いツールなので、三角関数の習い始めの頃にこういう定規を持っていたら面白かったなあ、と残念に思います。
