何これ!?コヒノール「数学テンプレート」18種のグラフが描ける製図定規
こんにちは、クリポンです。
先日「放物線定規」についてご紹介しました。記事の中であれこれとグラフを描いたのですが、久しぶりだったこともあり、随分と夢中になりました。
面白いツールを手に入れて自己満足していたところ、また新たに、謎の数学系定規を見つけました。見た目の奇妙さにびっくり、早速購入してみました。
今回はコヒノールのちょっと不思議な、数学系のテンプレート定規についてお届けします。
KOH-I-NOOR「テンプレート定規」使い方を解説!
世にも不思議な!?コヒノールのテンプレート
何だろうこれ?珍しい数学系のテンプレート定規です。

一目見て誰もが戸惑うのではないでしょうか。実はこれ、色々な関数のグラフが描けるテンプレートです。あるんですね、こういうものが。
チェコの文房具メーカー「コヒノール」が販売しています。ヨーロッパではこのような道具をテンプレートと呼びますが、日本語ではテンプレート、あるいは定規と言っても差し支えないと思います。
中高生を対象に作られた文房具だと思います。情報がなくて分からなかったのですが、学校指定で使うことがあるのかもしれませんね。
前にご紹介した数学系定規にも感心しましたが、今回の定規はさらにグレードアップ、その先を行っています。
前回ご紹介した数学系定規はこちらです:

テンプレートとは?
簡単に言えば「型」のことです。文房具としてのテンプレートは、正確にはステンシル テンプレート言います。単にステンシルと言ったりもします。
1枚の板に、型となる文字や図形が切り抜いてあり、上からなぞるだけで、素早くその形を写し取ることができます。
例えばこちらは音楽系のテンプレートです。

うまく書くのは結構難しいのですが、やってみるとなかなか楽しいです(笑)。
最近は、手帳用のテンプレートが増えているようです。絵を描くのが苦手という方でも、型があれば安心。ちょっとしたイラストを簡単に入れられます。
様々なものがあるので、探してみると好みのものが見つかるかもしれません。
18種の関数グラフを描いてみた!
テンプレート購入時に説明書は付いていませんでした。どうやって使うのだろう…まずはじっくり調べることから始めました。
その結果、18種もの関数のグラフが描けることが判明!主要な関数はほとんど網羅されています。その関数とは次の通りです。
|
私も興味津々!実際に18のグラフを描いていきます。
1次関数のグラフ
1. y=x
1次関数としましたが、何の事はない、直線定規として使える部分です。 左端に位置し、14cmあります。


2次関数のグラフ
2次関数が描く曲線は放物線と呼ばれます。コヒノールのテンプレートでは3種類の放物線が含まれています。
2. y=x2
最も基本となる放物線です。目印としてテンプレート上に「x2」と表示されています。

3. y=2x2
ここからはバリエーションです。x2の前に係数2を加えた放物線です。
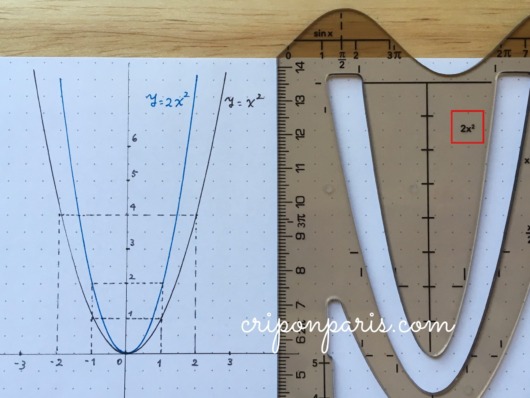
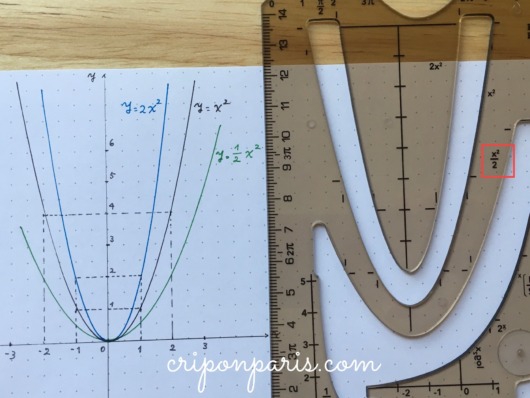
4. y=1/2x2
係数に分数1/2(2分の1)を取ると、緑の線になります。3種の放物線が描けました。
3次関数のグラフ
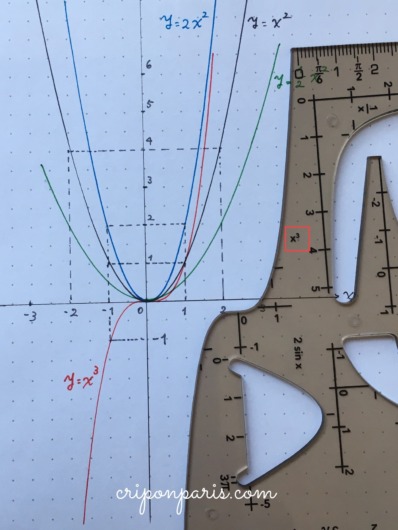
5. y=x3
テンプレートの端には、3次関数も用意されています。赤線で描いたのが、y=x3です。
三角関数のグラフ
6. y=sinx
三角関数においては、ぜひ覚えておきたい!4つのサインカーブが描けます。
まずは基本のy=sinx。

7. y=sin2x
sinxをsin2xとすることで、横の長さが半分(1/2)に縮小されます。
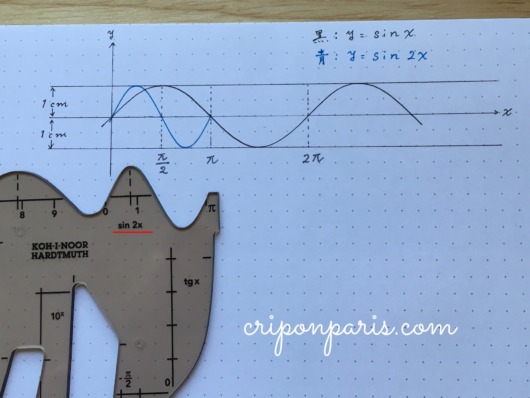
8. y=sin1/2x
sin1/2xとすると、sinxに比べて横の長さが2倍になります。
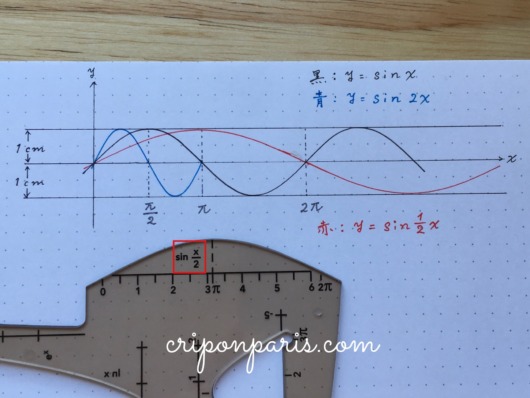
9. y=2sinx
sinxの前に2を加えると、振幅が2倍になります。sinxでは振幅1cmだったのが、2sinxでは2cmになりました。
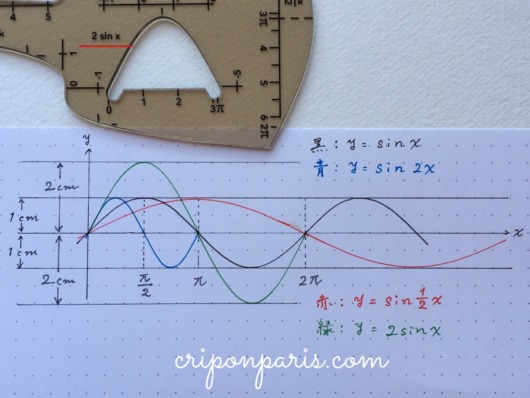
サインカーブだけを描きましたが、応用することでコサインカーブの作成も簡単です。
4つのコサインカーブも描けるとすると、このテンプレート1つで、22種の関数グラフが作れることになります。すごい!
10. y=tanx
忘れてはいけないタンジェントカーブ。テンプレートの端にあります。

分数関数のグラフ
11. y=1/x
18もの関数があるので、どこにあるのか見つけるのに迷うことも。テンプレート上で宝探しをしている気分です。
そうそうこの形の曲線!隅に小さく1/xと表示してありました。
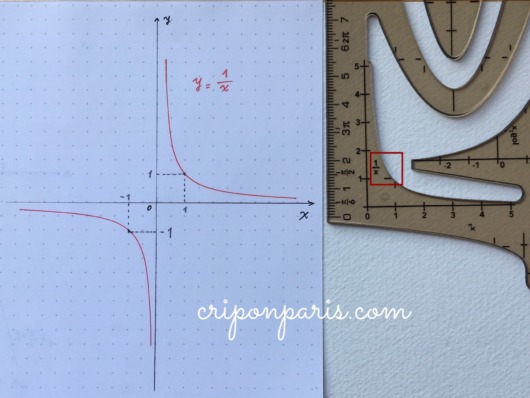
テンプレートには、原点とx軸、y軸が記されています。紙の上に自分で書いた軸と位置を合わせれば、ずれることなく綺麗なグラフができます。
指数関数のグラフ
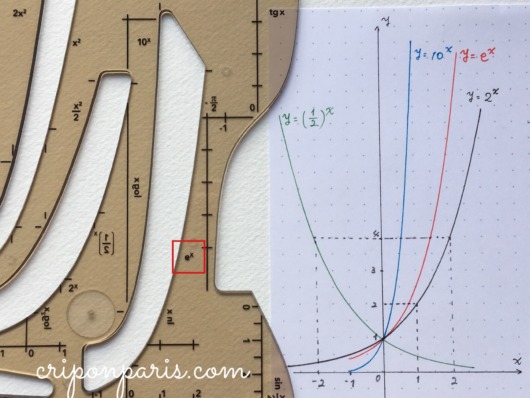
12. y=2x
なんと指数関数もあります。しかも4種の線が描けるんです。
まずは2xです。

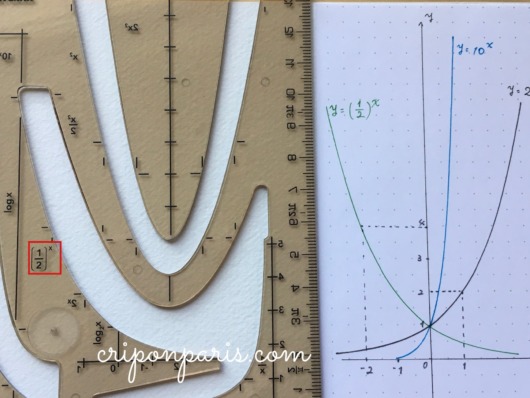
13. y=10x
次は10xです。

14. y=(1/2)x
2xとシンメトリーになる(1/2)xが用意されているのはいいですね。このテンプレートでは、2xを描く部分を裏返して(1/2)xとします。表裏で同じ場所を使う、関数を考えれば自然なことです。
15. y=ex
忘れてはいけない!ネイピア数も含まれています。
対数関数のグラフ
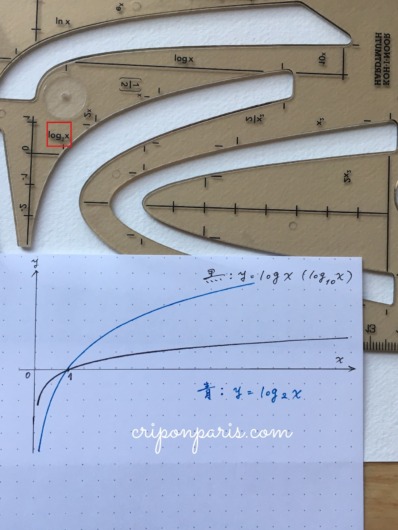
16. y=logx
指数関数ときたら、やはり対数関数。対数関数は、テンプレートを裏返して使います。
まずはy=logx、つまりlog10xのことです。

対数関数は指数関数の逆関数です。このテンプレート上では、指数関数を描く場所を、裏返して横に倒すことで、対応する対数関数が描けます。
例えば10xを描いた部分を裏返して横に倒すとlogxになります。
17. y=log2x
log2xは、先ほど指数関数2xを描いた場所を、ひっくり返して横に倒して使います。コヒノールのロゴが裏返っているのが見えます。
18. y=ln x
ln xは、logexのことです。

ln xはexの逆関数ということで、先ほどexを描いた場所を裏返して使います。
ガジェット好きにおすすめ
この関数グラフのテンプレートはすごい!よく考えて作られています。コンパクトにまとまっている上にデザイン的にも良いです。前回の放物線定規同様に、数学の勉強において、まあ、無くても構わない…というようなものですが、綺麗なグラフが作成できるのでまとめノートが作りやすい。ガジェット好きな生徒・学生さんは、勉強へのモチベーションが上がるかもしれませんね。




